一重項状態

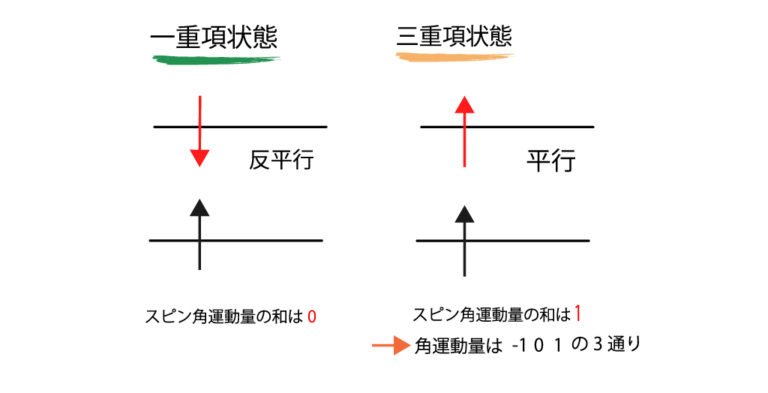
量子力学において、一重項（いちじゅうこう、英: singlet）とは、総スピンが0の量子状態を指す。この状態では、スピン成分の値は0しか許されない。

スピン1/2の粒子が2つあるとき、三重項と呼ばれる総スピンが1の状態が3通り${\displaystyle \uparrow \uparrow ,{\frac {1}{\sqrt {2}}}\left(\uparrow \downarrow \downarrow \uparrow \right),\downarrow \downarrow }$と、一重項と呼ばれる総スピンが0の状態が1通り${\displaystyle {\frac {1}{\sqrt {2}}}\left(\uparrow \downarrow -\downarrow \uparrow \right)}$存在しうる。理論物理学においては一重項とは、一次元表現（例えばスピン0の粒子）のことを指すことが多い。また、2つ以上の粒子が相互作用しあう系において、総角運動量がゼロの状態のことを一重項と呼ぶ場合もある。一重項やそれ以外の多重項は、粒子集団の総スピンが重要となる原子物理学や原子核物理学において頻繁に表われる。

単一の電子はスピン1/2を持ち、回転操作に対して二重項、つまりリー群SU(2) の基本表現として変換する。この電子状態のスピンは 作用素 ${\displaystyle {\vec {S}}^{2}}$ を状態に作用させることで得られ、必ず ${\displaystyle \hbar ^{2}\,(1/2)\,(1/2 1)=(3/4)\,\hbar ^{2}}$ が得られる。これは上向きスピン状態と下向きスピン状態はこの作用素の縮退した固有状態だからである。

同様に、電子が2つある場合の総スピンは作用素 ${\displaystyle \left({\vec {S}}_{1} {\vec {S}}_{2}\right)^{2}}$ を作用させることで得られる。ここで、 ${\displaystyle {\vec {S}}_{1}}$ は電子1に、 ${\displaystyle {\vec {S}}_{2}}$ は電子2に作用する作用素である。電子が2つの場合は、この総スピン状態の固有値は2通り、スピン0とスピン1に対応するものが存在する。それぞれの固有値に対応する固有状態は一つとは限らない。「スピン0」は一重項と呼ばれ、一つの固有状態にのみ対応する（後述）。これに対して「スピン1」は三重項と呼ばれ、3つの固有状態に対応する。

より数学的には、2つの二重項表現の積は随伴表現（三重項）と恒等表現（一重項）の和に分解することができると表現される。

一重項状態にある電子対は様々な性質を持つが、量子もつれに関連して、EPRパラドックスにおいて重要な役割を果たす。ディラック記法を用いると、EPR状態は通常以下のように表わされる。

${\displaystyle {\frac {1}{\sqrt {2}}}\left(\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle \right)}$

出典

関連項目

• 二重項状態
• 三重項状態
• スピン角運動量